Eine simple Theorie zu Covid19

Original (9.4.2020)
Ergänzungen (13.4.2020):

(27.4.2020):

(5.5.2020):

(5.5.2020):

(23.6.2020):

(1.8.2020):
(2.3.2021):

Daten update
Anpassung
Daten update
Ländervergleich
Daten update
UKUSSE
Daten update
Wellen-Theorie
Daten update
FR-Korrektur
Daten update
Nachtrag

Die Entwicklung jeder Epidemie gehorcht statistischen Gesetzen - die Form der statistischen Wachstumsfunktion F(t) wird bestimmt durch ihre Randbedingungen:

F(t gegen -unendl) = 0 und F(t gegen +unendl) = F₀ mit dF(t)/dt > 0.

Angewendet auf eine Epidemie bedeutet dies:

Die Anzahl der infizierten Menschen N(t) nimmt stetig zu.
Nach einer endlichen Zeit hat die Anzahl der infizierten Menschen ihren Höchstwert N₀ erreicht.

In der Physik wird ein derart begrenztes Wachstum mithilfe der Fermi-Dirac Statistik¹⁾ beschrieben und wir kennen für diese Statistik die Wachstumsfunktion F_F-D(t). Übertragen auf die Anzahl N(t) infizierter Menschen lautet diese:

N(t) = N₀/(exp(-2t/a) + 1),

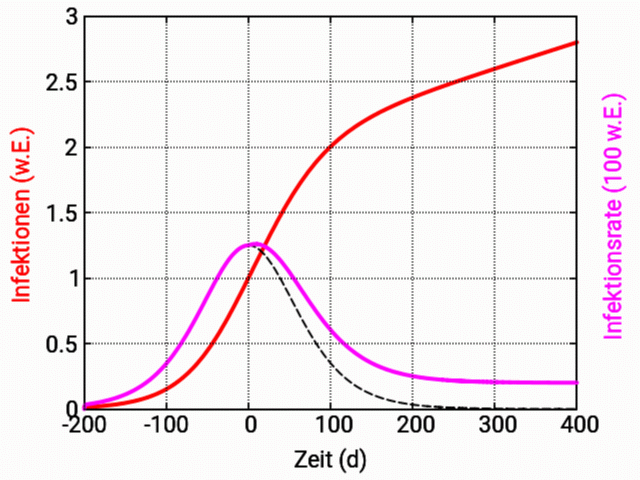
wobei die Zeitskala so gewählt ist, dass zur Zeit t=0 die Infektionsrate dN(t=0)/dt ihren Höhepunkt erreicht. Zu diesem Zeitpunkt ist die Anzahl der infizierten Menschen N(t=0) = N₀/2 ist, während die Infektionsrate dann dN(t=0)/dt = N₀/2a beträgt. Der Parameter a ist die charakteristische Zeit der Epidemie, er gibt die Zeitspanne an, während der die Anzahl infizierter Menschen von 27% auf 73% des Höchstwerts N₀ gestiegen ist. In der Abbildung unten habe ich N(t) für N₀ = 1 und a = 60 d (ca. 2 Monate) dargestellt - das epidemische Wachstum besitzt die Form, die man aus den Medien kennt, welche die gemessenen Daten publizieren²⁾. Ich habe mich nicht bemüht, N(t) an diese Daten anzupassen und so die Parameter N₀ und a zu bestimmen, denn noch sind die Daten zu ungenau und daher die Fehler der Anpassung zu groß. Aber die deutsche Regierung bemüht sich mithilfe von Verordnungen (Ausgehverbot, persönliche Abstandsregeln, etc), den Parameter a möglichst groß zu machen, um die Krankenhäuser zu entlasten. Ein Beispiel mag die Lage erläutern: Falls die BRD heute (8.4.2020) mit 1905 Toten den Höhepunkt der Corona Epidemie erreicht hat, dann kann man erwarten, dass sich bis zum Ende der Epidemie ca. 230000 Menschen infiziert haben werden. Steht der Höhepunkt noch vor uns oder liegt bereits hinter uns, verändern sich die Zahlen entsprechend. Und wie viele Menschen werden dann an den Infektionen gestorben sein?

Entwicklung der Infektionen (schwarz gepunktet), der Mortalität (rot gepunktet) und der relativen Mortalität (grün) in Abhängigkeit vom Parameterverhältnis b/a.

Das Infektionswachstum N(t) ist eigentlich nicht so interessant, interessanter ist das Mortalitätswachstum M(t), d.h. die Anzahl der Menschen, die aufgrund der Infektion sterben. Denn würden die Infektionen nicht auch zum Tode führen, wären sie für unsere Gesellschaft von nur geringer Bedeutung.

Auch die Eigenschaften von M(t) lassen sich mit statistischen Methoden untersuchen. Und da auch in diesem Fall dieselben Randbedingungen gelten, die ich bereits oben spezifiziert hatte, ist klar: Die Basis für eine Untersuchung bildet wiederum die Fermi-Dirac Statistik mit der Wachstumsfunktion F_F-D(t), allerdings mit anderen Parametern:

Die Menschen werden erst mit einer gewissen Zeitverzögerung ðt nach der Infektion sterben.
Nicht alle Menschen, die sich infiziert haben, werden sterben, sondern nur ein Bruchteil x von N₀.
Die charakteristische Zeit b der Mortalität hängt von der Krankenbetreuung ab - ist das Krankenhaus nur schlecht ausgestattet, wird b < a gelten, ist es aber gut ausgestattet, kann auch b > a gelten.

Daher sollte das Mortalitätswachstum durch folgende Funktion beschrieben sein:

M(t) = xN₀/(exp(-2(t-ðt)/b) + 1).

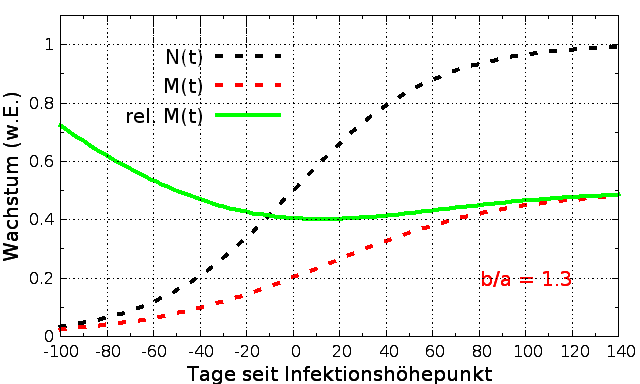
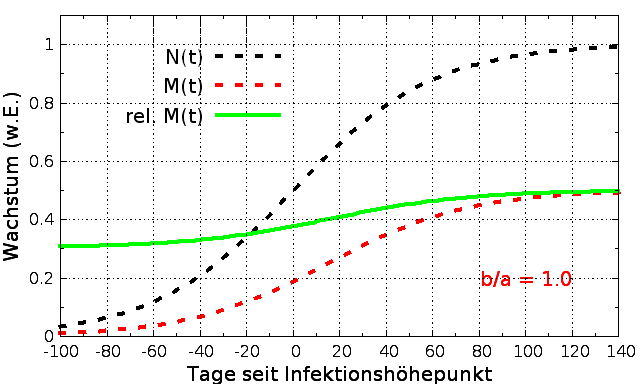
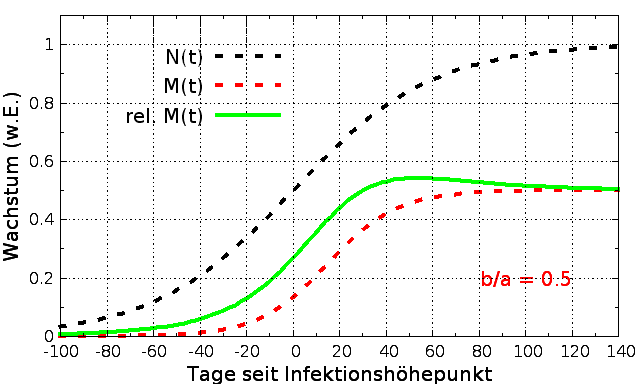
Die Abbildungen oben zeigen M(t) für x = 0.5 , ðt = 15 d und für 3 verschiedene Werte des Zeitverhältnisses b/a. Und noch interessanter wird es, wenn man nicht M(t) selbst, sondern normiert auf die Anzahl der Infektionen, d.h. die relative Mortalität rel. M(t) = M(t)/N(t) untersucht. Dann wird auch klar, wie gut Länder auf den Ausbruch der Epidemie vorbereitet waren und wie effektiv ihre Abwehrmaßnahmen waren. Auch rel. M(t) ist in den Abbildungen oben dargestellt, ihr zeitlicher Verlauf ändert sich stark mit dem Wert des Zeitverhältnisses b/a.

Gemäß der Fermi-Dirac Statistik muss das Epidemiewachstum N(t) die charakteristische Eigenschaft besitzen, dass die Wachstumsrate dN(t)/dt symmetrisch um die Zeit t=0 des Epidemiehöhepunkts ist, d.h. dN(-t)/dt = dN(+t)/dt. Wie wir gleich erkennen werden, haben die gemessenen Daten diese Eigenschaft NICHT, die maximale Anzahl von Infizierten wird erst zu Zeiten erwartet, die viel später sind als es diese Symmetrieregel vorschreibt. Angenommen, die hier vorgestelllte Theorie ist anwendbar (und ich zweifele daran nicht!), ist die gemessene Asymmetrie ein Hinweis darauf, dass sich das Infektionswachstum in mehreren Wellen vollzieht, d.h. der 1. Welle folgt später eine 2. Welle und u.U. noch mehrere weitere Wellen.

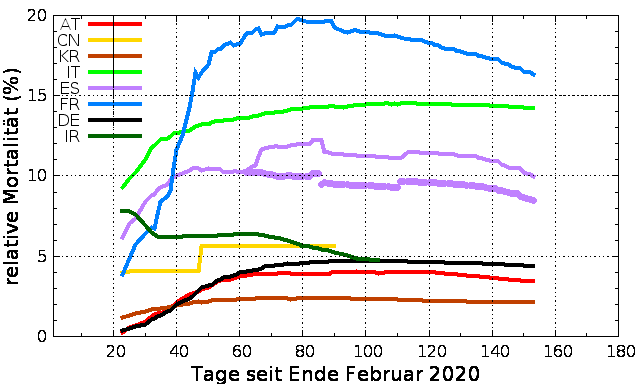
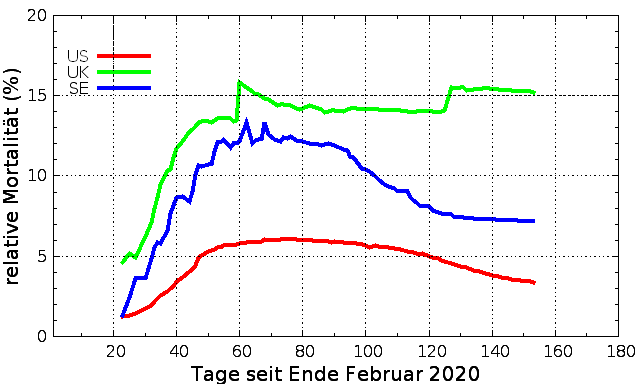
Bisher sind dies alles nur theoretische Überlegungen. Es wird Zeit, dass ich die tatsächlich gemessenen Daten betrachte. Ich habe 11 Länder ausgewählt, die entsprechenden Daten habe ich meiner lokalen Zeitung (Rhein-Neckar-Zeitung) entnommen. Begonnen mit der Datenanalyse habe ich am 23.3.2020, ab dann habe ich die relativen Mortalitäten berechnet, wie sie für 8 Länder in der Abbildung rechts dargestellt sind. Das sind:

Österreich(AT), China(CN), Südkorea(KR), Italien(IT), Spanien(ES), Frankreich(FR), Deutschland(DE), Iran(IR).

Die Entwicklung der relativen Mortalitäten ist recht aufschlussreich: Unter den europäischen Ländern hat es Frankreich wohl am schlimmsten getroffen, nachdem am 11.4. die französischen Daten für die Anzahl infizierter Menschen nach unten korrigiert wurden und dadurch die relative Mortalität um ca. 25% angestiegen ist. Das bedeutet, dass in diesem Land etwa 20% der nachgewiesenen Covid19-Patienten sterben werden - sicherlich kein Gütezeichen für das französische Gesundheitssystem. In der BRD war die Lage wesentlich besser - nur ca. 5% werden dort wohl sterben.

In dieser Ländergruppe sind die Mortalitätsverläufe ziemlich ähnlich, wenn man sie auf einen gemeinsamen Bruchteil x von N₀ normiert. Der Vergleich mit den Abbildungen oben weist aber darauf hin, dass für sie b < a gilt, d.h. keines dieser Länder wahr hinreichend auf den Ausbruch der Epidemie vorbereitet.

Der zeitliche Verlauf der relativen Mortalitäten in 8 verschiedenen Ländern. Ab dem 1.5.20 habe ich die Daten für Spanien(ES) ergänzt durch jene, die ich der Ref. in Fußnote²⁾ entnommen habe(gepunktet). Vielleicht als Beispiel für die Vertrauenswürdigkeit der publizierten Daten!

Von den ausgewählten nichteuropäischen Ländern beobachtet man dagegen ein abweichendes Verhalten:

China hat offensichtlich das Ende der Epidemie erreicht, hat seine Statistik aber Mitte April korrigieren müssen (kann man diesen Daten überhaupt trauen?). Demnach sind bis zum 1.6.2020 ca. 6% der Infizierten verstorben, danach habe ich die Daten nicht weiter verfolgt.
Südkorea steht kurz vor dem Ende, dieses Land war gut auf die Epidemie vorbereitet, der Anteil der Verstorbenen beträgt nur 2%. Aber die Ausbreitung der Epidemie in diesem Land, wie auch in den meisten anderen Ländern, weist Besonderheiten auf, die ich später weiter kommentieren werde.
Der Iran zeigt einen total unterschiedlichen Mortalitätsverlauf, was nach der Abbildung oben auf b > a hindeutet. Dass dies durch ein gutes Gesundheitssystem erreicht wird, ist unwahrscheinlich. Eine bessere Erklärung ist wohl, dass das Durchschnittsalter der iranischen Bevölkerung bei 28 a liegt und Iraner daher widerstandsfähiger gegen die Folgen der Infektion sind³⁾. Vorausgesetzt, die Daten sind korrekt, kann die stetige Abnahme der relativen Mortalität bis zum 10.6.2020 nur bedeuten, dass die Anzahl der Infektionen wieder zunimmt und der Iran den Höhepunkt der Epidemie noch nicht überschritten hat. Wie bei China gilt auch hier: Danach habe ich die Daten nicht weiter verfolgt.

Dies alles gilt natürlich nur unter der Voraussetzung, dass die Daten korrekt sind. Und auch den Einwand, dass meine Theorie zu simpel sei, kann ich nicht zurückweisen: Man kann es komplizierter machen und eine System von gekoppelten Differentialgleichungen¹⁾ lösen, das die Bedingen für Infektion Mortalität und Genesung beschreibt, die alle miteinander verknüpft sind. Aber dann würde ich immer noch rechnen, während die Epidemie längst vorüber ist!

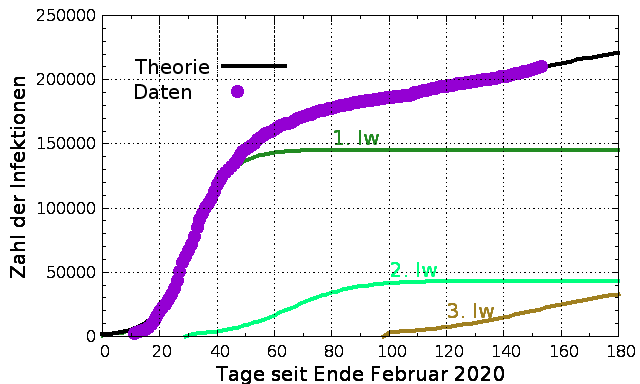
Heute (1.8.2020) sind mehr als 5 Monate seit dem Ausbruch der Epidemie in der BRD vergangen - Zeit, zum letzten Mal ihren Verlauf mit den theoretischen Vorhersagen zu vergleichen. Danach werde ich Analysen erst wieder vornehmen, wenn wirkliche dramatische Entwicklungen beobachtet werden sollten, die zu einem erneuten Stillstand des öffentlichen Lebens führen.

Die Abbildung unten zeigt die Anpassung von N(t) an die Daten, welche ich diesmal der in Fußnote 2) genannten Referenz entnommen habe. Die Theorie reproduziert die Daten recht genau, falls man davon ausgeht, dass 3 Infektionswellen aufgetreten sind:

1. Welle:
Der Tag des Epidemiehöhepunkts war um den 1.4. (t₀= 31.5±0.5 d) und die charakteristische Zeit ihrer Ausbreitung betrug a = 13±2 d.
2. Welle:
Diese Welle ereignete sich ca. 1 Monat später (t₀ = 65±0.5 d) und ihre charakteristische Zeit betrug a = 22±2 d.
3. Welle:
die Ursache dieser Welle lässt sich recht genau angeben: Nichtbeachtung der Restriktionen ganz allgemein, aber insbesondere bei Gottesdiensten, Familienfeiern und in der Fleischindustrie. Die charakteristischen Parameter sind (geschätzt) t₀= 150±2d und a=40±2d.
Die maximale Anzahl der in der BRD infizierten Menschen wird sich dadurch auf N₀ = 230000 ± 2000 erhöhen.

Anpassung von N(t) an die tatsächliche Anzahl von Infizierten in der BRD. Infektionswellen sind mit Iw abgekürzt.

Wichtig sind die Fehlerangaben, die einer Standardabweichung entsprechen, d.h. das zu erwartende Ergebnis liegt mit 68% Wahrscheinlichkeit innerhalb dieser Fehlergrenzen. Die Ursachen für das Auftreten der 2. Infektionswelle in der BRD ist unbekannt. Vielleicht war eine der Ursachen das Verlangen vieler Politiker, die durch die Epidemie verfügten gesellschaftlichen und wirtschaftlichen Beschränkungen langsam zurückzunehmen, denn öffentlich wird der Protest ihrer Wähler gegen diese Beschränkungen immer hörbarer. Und es kann nicht ausgeschlossen werden, dass die BRD auch in Zukunft von weiteren Infektionswellen erfasst wird (wie in Südkorea).

Und noch eine Bemerkung zur Anpassung der Theorie an die Daten: Statistische Methoden wurden entwickelt, um Datenmengen mit statistischen Schwankungen zu analysieren. Die Frage, ob diese Daten korrekt sind oder nicht, ist bedeutungslos - sie sind per Definition immer korrekt. Die Fehlergrenzen, die mithilfe der Anpassung der Theorie an die Daten berechnet werden, fallen in die Kategorie der "statistischen Fehler". Sie sind zu unterscheiden von den "systematischen Fehlern" (auch Systemfehler), die sich aus systematisch falschen Daten ergeben. Derartige Systemfehler resultieren z.B. aus einer Änderung des Messverfahrens während der Messung. Im Falle einer Epidemie kann das eine Ausdehnung der getesteten Personengruppe sein oder eine Änderung der Testmethode selbst. Systemfehler sind i.A. erkennbar an der systematischen Abweichung der Daten von der Theorie. Meine Bemerkung zur Korrektheit der Daten am Ende des letzten Kapitels bezog sich aber auf die weitere Möglichkeit, das nicht-demokratische Staaten versucht sein könnten, ihre Daten zu manipulieren, d.h. zu fälschen, um die Überlegenheit ihres Gesellschaftssystems zu "beweisen". Dass die BRD zu diesen Staaten gehört, ist wohl eher nicht zu vermuten.

Nach der BRD habe ich für 6 weitere Länder die Anpassung von N(t) an ihre Epidemiedaten vorgenommen - diese Daten sind vom Typ her ähnlich zu denen der BRD und ich zeige daher nicht für jedes dieser Länder die entsprechenden Abbildungen. Aber die Tabelle unten enthält die charakteristischen Parameter der jeweiligen Epidemie: Die Ausbreitungsgeschwindigkeit v = 1/a (Fehler ±0.2v²), den Tag des Höhepunkts t₀ (Fehler ±0.5 Tage), das zu erwartende Infektionsmaximum N₀ (Fehler ±0.02N₀) und die relative Mortalität, die ich allerdings nur aus der Abbildung oben geschätzt habe.

Parameter	Südkorea	Österreich	BRD	Frankreich	Großbritannien	Schweden	USA
v (d^-1)	1. Iw: 0.17 2. Iw: 0.06 3. Iw: 0.10 4. Iw: 0.03	1. Iw: 0.09 2. Iw: 0.03 3. Iw: 0.05	1. Iw: 0.08 2. Iw: 0.05 3. Iw: 0.04	1. Iw: 0.06 2. Iw: 0.03 3. Iw: 0.05	1. Iw: 0.04	1. Iw: 0.04 2. Iw: 0.05	1. Iw: 0.04 2. IG: 0.03 3. Iw: 0.04
t₀	1. Iw: 02.03. 2. Iw: 29.03. 3. Iw: 19.05. 4. Iw: 01.07.	1. Iw: 27.03. 2. Iw: 14.05. 3. Iw: 20.07.	1. Iw: 01.04. 2. Iw: 04.05. 3. Iw: 28.07.	1. Iw: 04.04. 2. Iw: 08.06. 3. Iw: 07.08.	1.Iw: 27.04.	1. Iw: 24.04. 2. Iw: 19.06.	1. Iw: 24.04. 2. IG: 18.06. 3. Iw: 23.07.
N₀ (pro Einwohner)	14.8 Tsd. (0.031%)	22.4 Tsd. (0.27%)	228 Tsd. (0.28%)	213 Tsd. (0.33%)	305 Tsd. (0.45%)	80 Tsd. (0.78 %)	5.9 Mio. (1.90%)
rel. Mortalität	2.10%	3.40%	4.35%	16.33%	15.22%	7.14%	3.39%

Charakteristische Parameter von N(t) nach der Anpassung an den tatsächlichen Epidemieverlauf von 6 verschiedenen Ländern. Die Reihenfolge der Länder wird bestimmt durch den Zeitpunkt t₀ des Höhepunkts der 1. Infektionswelle (abgekürzt Iw).

Südkorea stellt insofern einen Sonderfall dar, als der Epidemieverlauf in diesem Land darauf hinweist, dass es sich um eine Quadrupelepidemie gehandelt hat: Der 1. Infektionswelle sind 3 weitere Infektionswellen gefolgt, wobei die Ursachen der 2. und 4. Welle unbekannt sind, die der 3. aber wohl bekannt: Ein 29 jähriger Koreaner hat Anfang Mai bei seiner nächtlichen Tour durch zahlreiche Bars in Seoul mehr als 100 Personen infiziert, die Gesamtzahl der Infizierten stieg um ca. 500 Personen.

Dies ist ein Ereignis, dass die deutsche Regierung auf jeden Fall vermeiden wollte, indem die Rücknahme der von ihr verfügten Verordnungen nicht zu schnell erfolgen sollte. Das ist ihr offensichtlich aber nicht gelungen.

Anpassung von N(t) an die tatsächliche Anzahl von Infizierten in Südkorea. Infektionswellen sind mit Iw abgekürzt.

Denn die Öffentlichkeit fügt sich sich den verordneten Restriktionen nur für eine gewisse Zeit, danach wird sie den Beschränkungen in ihrem Leben überdrüssig und revoltiert - ein soziologisches und kein gesundheitspolitisches Problem, für das es wohl keine Lösung gibt. Und das zweifeln lässt, ob die 1. fünf Länder in obiger Tabelle die Covid19-Epidemie tatsächlich schon überwunden haben.

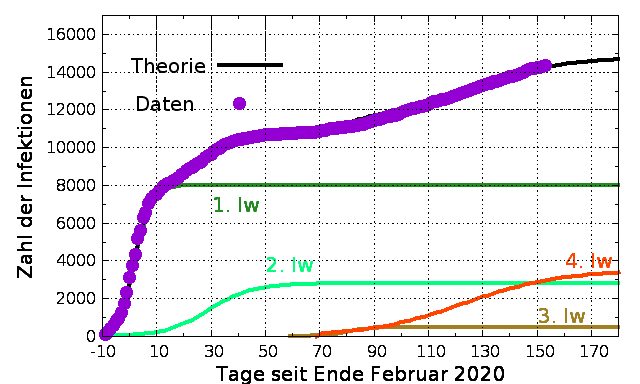
Denn in Südkorea hat es derartige Verordnungen sicherlich auch gegeben⁴⁾. Und in Südkorea waren sie, trotz der 4 Infektionswellen, recht erfolgreich:

Nur 0.031% der Gesamtbevölkerung wurde infiziert.
Nur 0.0006% der Gesamtbevölkerung ist an den Folgen der Infektion gestorben.

Erklärt wird dies damit, dass Südkoreaner rigoros auf Covid19 getestet wurden und Infizierte frühzeitig erkannt und behandelt wurden. Erklärt wird damit aber nicht, warum dort die stattlichen Maßnahmen wirksamer waren und noch sind als z.B. in der BRD. Und diese Frage stellt sich insbesondere bei den 3 Ländern, die ich zum Schluss betrachten will.

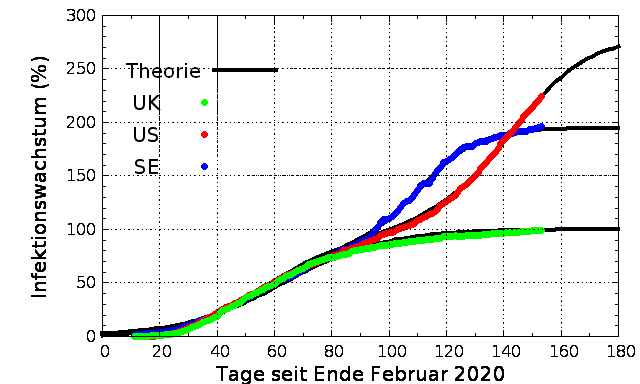
Großbritannien(UK), die USA(US) und Schweden(SE) wurden am spätesten von der Corona-Epidemie erreicht. Diese 3 Länder sind in mehrerer Hinsicht interessant:

UK: Strikte Maßnahmen gegen die Ausbreitung der Epidemie wurden vom Staat erst angeordnet, nachdem Premierminister Johnson selbst an Covid19 erkrankt war.
US: Die Gouverneure der Einzelstaaten mussten staatliche Restriktionen gegen die Anordnungen ihres Präsidenten Trump durchsetzen, der dagegen mehr wirtschaftlichen Interessen folgt.
SE: Maßnahmen gegen die Virusinfektionen wurden nur beschränkt vom Staat verordnet, sie wurden i.W. der Eigenverantwortung der schwedischen Bevölkerung überlassen.

Diese Methoden kontrastieren stark gegen jene, welche z.B. von Frankreich seinen Bürgern zugemutet wurden und welche dort das gesellschaftliche und wirtschaftliche Leben extrem einschränkten. Sind diese unterschiedlichen Vorgehensweisen in den charakteristischen Parametern der Covid19-Ausbreitung zu erkennen?

Die Daten (siehe Abbildung unten links) zeigen, dass in den UK/US/SE-Ländern die Ausbreitungsgeschwindigkeiten zunächst sehr ähnlich waren.

Der prozentuale Anstieg der Infektionen in den UK/US/SE Ländern.

Der Verlauf der relativen Mortalitäten in den UK/US/SE Ländern.

Diese Abbildung verdeutlicht aber auch, dass nach ca. 2 Monaten die Infektionszahlen stark voneinander abweichen:

In UK nähern sie sich dem Grenzwert N₀.
In US zeigt sich ein fast linearer Anstieg der Infektionszahlen, ohne dass ein Grenzwert zu erkennen wäre.
In SE lässt sich der Verlauf nur so interpretieren, dass eine 2. Infektionswelle entstanden ist, deren Ende aber u.U. zu erkennen ist.

Und daher sind auch die relativen Mortalitäten dieser 3 Länder (Abbildung oben rechts) wenig aussagekräftig: Die Abnahme von rel. M(t) in SE kann durchaus eine Folge der starken Zunahme an Infektionen sein.

Lässt sich anhand dieser Daten irgendeine Aussage darüber machen, ob staatlich verordnete Restriktionen den Verlauf der Corona-Epidemie wesentlich beeinflusst haben? Ich meine: Nein. Wenn überhaupt, lassen sich 3 Länderkategorien erkennen:

Südkorea hat die Ausbreitung des Coronavirus am besten unterdrückt, obwohl dort bisher 4 Infektionswellen auftraten.
Österreich, Deutschland und Frankreich haben eine relativ geringe Anzahl von Infizierten, aber in Frankreich ist die Anzahl der Verstorbenen besonders hoch, was wahrscheinlich auf ein schlechtes Gesundheitssystem zurückzuführen ist.
Die UK/US/SE-Länder zeigen zunächst ein ähnliches, dann aber sehr unterschiedliches Verhalten. Man kann vermuten, dass (nach der anfänglichen Nachlässigkeit) die Gefahren von Covid19 sehr unterschiedlich beurteilt wurden, und die Beschneidung von Freiheitsrechten bzw. der wirtschaftliche Rückgang als größere Gefahren betrachtet wurden.

Die Vorstellung, dass sich nur genügend viele Einwohner eines Lands infizieren müssten, um eine Virusresistenz aufzubauen und so den Grenzwert N₀ zu erreichen, halte ich für eine unbewiesene und gefährliche Behauptung. Und das ist auch keine Antwort auf die Frage, wie groß ist N₀ und lässt sich dieser Wert durch demokratische Maßnahmen festlegen. Und so beschleicht mich das Gefühl, dass meine Studie, die viel Zeit gekostet hat, doch eigentlich nutzlos ist, weil sich das Coronavirus nicht an die demokratischen Spielregeln hält und wir nicht bereit sind, diese Spielregeln deswegen abzuschaffen.

Und außerdem sollte bedacht sein: Grundlage meiner Analyse der Covid19-Infektionen ist die Wellentheorie, die davon ausgeht, dass jede Infektionswelle durch einer maximalen Anzahl N₀ von Infizierten in einem lokal begrenztem Gebiet definiert ist. Politisch soll diese Vorgabe mithilfe des "lock-downs" realisiert werden. Aber die Daten oben haben gezeigt, dass diese Analyse zu viel mehr Infektionswellen führt als politisch opportun erscheint. Mit anderen Worten: Der "lock-down" funktioniert nicht, z.B. wegen der Zuwanderung Infizierter aus anderen Gebieten. Dann erscheint eine alternative Beschreibung des Infektionsgeschehens sinnvoller, welche die Anzahl der Wellen wesentlich verringert (wie die Politik es wünscht), dann aber annimmt, dass N₀ nicht zeitlich konstant ist, sondern zunimmt. Was aber auch bedeutet, dass sich Infektionsgebiete ausbreiten, also nicht mehr lokalisieren lassen. Welche funktionale Darstellung N₀(t) besitzt, ist theoretisch nicht vorhersehbar, sondern unterliegt politischen Vorgaben, etwa der Lockerung des "lock-downs" in den einzelnen Bundesländern.

Zur Illustration zeigt das Bild rechts die Anzahl N(t) von Infektionen und die Infektionsrate dN(t)/dt unter der willkürlichen Annahme, dass N₀(t) linear ansteigt, nachdem dN(t)/dt zur Zeit t=0 d denn maximalen Wert erreicht hat. Vergleicht man dieses Ergebnis mit den publizierten Daten, so wird deutlich, dass es in vielen Fällen der tatsächlichen Ausbreitung der Covid19-Epidemie entspricht, z.B. in den bereits oben dargestellte Fällen Südkorea und Österreich. Ich habe mir trotzdem nicht die Mühe gemacht, daraus den zeitlichen Verlauf von N₀(t) zu extrahieren, denn dieser ist eigentlich uninteressant - interessant ist allein, dass es bisher in keinem Fall gelungen ist, N₀(t) zu begrenzen. Und die Daten geben auch keinen Hinweis darauf, wie groß dieser Grenzwert sein mag und wann er endlich erreicht sein könnte.

Die Datenanalyse wäre noch komplizierter, wenn auch die Ausbreitungsgeschwindigkeiten v(t) der Epidemie zeitlich variieren sollten, etwa weil neue und aggressivere Mutationen des SARS-CoV-2 auftreten. Diese Variationen wären nicht zu unterscheiden von politischen Gegenmaßnahmen im Rahmen eines "lock-downs", sie machen aber eine wissenschaftliche Analyse der Ausbreitung praktisch unmöglich. Insbesondere ergeben sich keine Hinweise daraus, was die Ausbreitung hemmen könnte.

Die Anzahl von Infektionen und die Infektionsrate nach der Modifikation der F.-D. Statitistik. Zum Vergleich ist die unmodifizierte Infektionsrate (schwarz-gestrichelt) gezeigt.

Lernen wir dann allein aus den Daten mehr? Die Tabelle unten ist Anfang März 2021 entstanden und sollte verglichen werden mit der entsprechenden Tabelle oben von Anfang August 2020.

Parameter	Südkorea	Österreich	BRD	Frankreich	Großbritannien	Schweden	USA
N₀ (pro Einwohner)	90.8 Tsd. (0.176%)	462.8 Tsd. (5.22%)	2.46 Mio. (2.97%)	3.78 Mio. (5.65%)	4.19 Mio. (6.28%)	889 Tsd. (6.54 %)	29.37 Mio. (8.95%)
rel. Mortalität	1.77%	1.86%	2.90%	2.31%	2.94%	1.93%	1.80%

Siehe Tabelle oben.

In diesem halben Jahr:

Hat sich die Anzahl der Infektionen in allen Ländern erhöht, am geringsten in den USA(500%), am stärksten in Österreich(2000%). Bezogen auf die jeweiligen Bevölkerungszahlen gab es Anfang März 2021 etwa 5-9% Infizierte (Deutschland 3%), mit der auffälligen Ausnahme von Südkorea mit nur 0.2% Bevölkerungsanteil. Was zeichnet Südkorea aus? Vermutlich die rigorose Identifikation und Kontaktverfolgung von Infizierten, die so in Deutschland aufgrund der Datenschutzbestimmungen unmöglich wäre.
Sind die relativen Mortalitäten jetzt etwa gleich hoch (ca. 2%). Auch in Frankreich und Großbritannien haben sie sich auf diesen Wert eingependelt.

In allen Ländern waren die Maßnahmen gegen die Ausbreitung von SARS-CoV-2 sehr unterschiedlich und keine der Strategien war offensichtlich besonders erfolgreich. Insbesondere ist nicht zu erkennen, dass Schweden, das den "lock-down' weitest gehend vermieden hat, besonders schlecht dastünde.

¹⁾ An anderer Stelle habe ich mich mit der Frage beschäftigt, welche Statistiken in der Natur von fundamentaler Bedeutung sind.
²⁾ Wer nach aktuellen Daten sucht, hier kann man sie finden (in englisch).
³⁾ Diese Erklärung hat mir Rötger Nötzel geschickt, dem ich dafür sehr danke.
⁴⁾ Warum aber Bars und Clubs nicht geschlossen wurden, ist mir ein Rätsel.

Nachfragen bitte richten an: dietrich.pelte@web.de