Ich habe bisher zur Beschreibung des Abbaus der fossilen Energievorräte bis in das Jahr 2050 und ganz allgemein für jedes limitierte Wachstum immer die epidemische Wachstumsfunktion (
| df(x)/dx = f(x) (a - b f(x)) | (1) |
- Maxwell-Boltzmann Statistik (klassische Statistik) für a < 0 und b = 0. Für a > 0 und b = 0 entspricht dies einem grenzenlosen Wachstum.
- Fermi-Dirac Statistik (Quantenstatistik der Fermionen) für a < 0 und b = 1. Für a > 0 und b > 0 entspricht dies einem limitierten Wachstum.
- Bose-Einstein Statistik (Quantenstatistik der Bosonen) für a < 0 und b = -1. Für a > 0 und b < 0 entspricht dies einem stimulierten Wachstum.2)
 Buch diskutiert. Niemand wird
behaupten können, dass dies ein reiner Zufall sei und nicht
eine, von der Natur vorgegebene Methode ihrer Beschreibung.
Und in diesem Sinne habe ich die obige Differentialgleichung
auch zur Beschreibung des limitierten Wachstums benutzt: Es
ist eine von der Natur angebotene Methode zur Beschreibung
von Prozessen, welche sich nur innerhalb fester und
endlicher Grenzen entwickeln können.
Buch diskutiert. Niemand wird
behaupten können, dass dies ein reiner Zufall sei und nicht
eine, von der Natur vorgegebene Methode ihrer Beschreibung.
Und in diesem Sinne habe ich die obige Differentialgleichung
auch zur Beschreibung des limitierten Wachstums benutzt: Es
ist eine von der Natur angebotene Methode zur Beschreibung
von Prozessen, welche sich nur innerhalb fester und
endlicher Grenzen entwickeln können.| dW(t)/dt = G(t) - V(t) | (2) |
untersucht, welche
ich z.B. auch in  Kap. 6.3
benutze. Die Funktion G(t) ist der
Gewinnterm, - V(t) ist der
Verlustterm und hat daher ein negatives Vorzeichen. Mit
G(t) = a W(t) und V(t) = b/a W2(t) gehört auch das
epidemische Wachstum zu dieser Klasse von
Differentialgleichungen. Interessanter für die
augenblickliche Diskussion sind jedoch solche Fälle, in
denen G(t) oder V(t) nicht selbst
Funktionen von W(t) sind, sondern
menschliches Verhalten modellieren. Dies gilt
insbesondere für den Gewinnterm G(t), der als
Spiegelbild menschlicher Aktivitäten innerhalb von
begrenzten Ressourcen die Bedingung G(t) = 0 für t < 0 und t
->
Kap. 6.3
benutze. Die Funktion G(t) ist der
Gewinnterm, - V(t) ist der
Verlustterm und hat daher ein negatives Vorzeichen. Mit
G(t) = a W(t) und V(t) = b/a W2(t) gehört auch das
epidemische Wachstum zu dieser Klasse von
Differentialgleichungen. Interessanter für die
augenblickliche Diskussion sind jedoch solche Fälle, in
denen G(t) oder V(t) nicht selbst
Funktionen von W(t) sind, sondern
menschliches Verhalten modellieren. Dies gilt
insbesondere für den Gewinnterm G(t), der als
Spiegelbild menschlicher Aktivitäten innerhalb von
begrenzten Ressourcen die Bedingung G(t) = 0 für t < 0 und t
-> 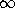 erfüllen
muss3). Um für den Abbau der fossilen
Ressourcen eine eindeutige Nomenklatur zu bilden, wird
erfüllen
muss3). Um für den Abbau der fossilen
Ressourcen eine eindeutige Nomenklatur zu bilden, wird
- G(t) als Exploration bezeichnet,
- dW(t)/dt als Extraktion bezeichnet,
- W(t) =
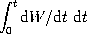 als Kumulation bezeichnet.
als Kumulation bezeichnet.
1. Exponentielle Exploration.
Dies ist eigentlich kein Modell, dass menschlichen Aktivitäten besonders gut angepasst ist. Ich habe es zur Demonstration gewählt, weil
- auch dieses Modell ein W(t) ergibt, das nur wenig Abweichungen vom epidemischen Wachstum zeigt,
- die sich ergebende Differentialgleichung analytisch
integrabel ist und ein Korrelat in der Natur besitzt,
nämlich den radioaktiven Zerfall innerhalb einer
Mutter-Tochter Kette. Eine Behandlung dieses Zerfalls
findet man z.B. in
 meinem Buch.
meinem Buch.
| In diesem Modell ist G(t) = a exp(-bt) für positive Zeiten, V(t) = c W(t) für positive Extraktion. Die analytische Lösung für die Extraktion lautet dW(t)/dt
sie ist mitsamt der zugehörigen Kumulation in der Abbildung rechts dargestellt. Die Parameter a, b, c sind so gewählt, dass letztere eine gute Übereinstimmung mit dem epidemischen Wachstum zeigt, das in der rechten Abbildung zum Vergleich ebenfalls gezeigt wird. Natürlich kann diese Übereinstimmung nicht vollkommen sein, wie die Extraktionskurven recht gut zeigen. Auf der anderen Seite werden durch die Integration die Differenzen weitgehend ausgeglichen. |
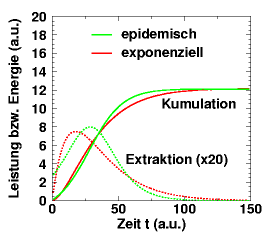 Die Extraktions- und Kumulationskurven für 2 verschiedene Wachstumsmodelle (epidemische und exponentiell, siehe Text). |
Viel näher menschlichem Verhalten ist natürlich eine Explorationskurve, welche im Intervall 0
 t
t
 t0
ein Maximum besitzt.
t0
ein Maximum besitzt.| In einer einfachen
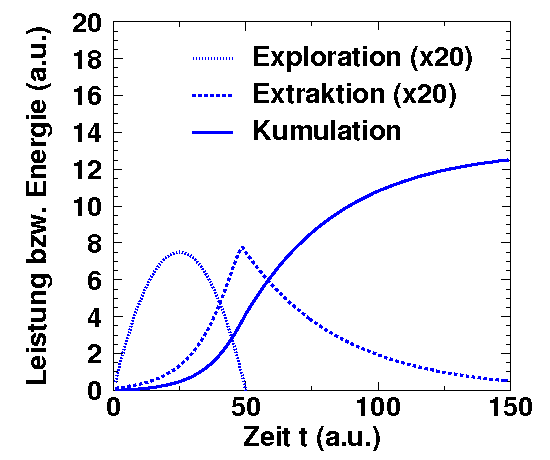
Näherung ist dies die quadratische Funktion G(t) = at (1 - t/b) mit b = t0.
Die sich daraus ergebende Differentialgleichung ist vermutlich auch analytisch integrabel. In Zeiten, da fast jeder einen PC besitzt, ist die numerische Integration aber viel einfacher, die Ergebnisse dieser Integration in Bezug auf Exploration, Extraktion und Kumulation sind in der Abbildung rechts dargestellt. Wie erwartet, ähnelt die Kumulationskurve den Kurven, welche mit den beiden vorher benutzten Modellen berechnet wurden. Die zeitliche Verschiebung zwischen der Explorations- und der Extraktionskurve ist aber ein Verhalten, das auch tatsächliche Daten über die Erdölförderung zeigen (siehe z.B. |
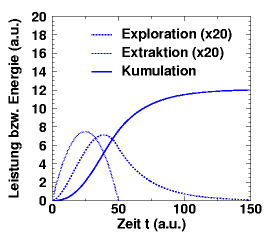 Das
Versorgungsmodell mit quadratischer
Explorationsfunktion.
|
- Je höher der Energiepreis, um so stärker werden
Fördergesellschaften dazu neigen, auch sonst unrentable
Energieträger zu extrahieren. In einfacher Näherung dW(t)/dt
 P(t).
P(t). - Je höher der Energiepreis, um so stärker werden Nutzer
versuchen, durch Sparmaßnahmen ihren Energiebedarf zu
reduzieren. In einfacher Näherung V(t)
 (P(t))-1.
(P(t))-1.
| P(t) |
(3) |
| dW(t)/dt = (a G(t) - b V(t) (P(t))-1) P(t) = (a G(t) P(t) - b V(t)) | (4) |
Es ist nicht versucht worden, dieses
Versorgungsmodell an existierende Daten anzupassen,
sondern es soll nur prinzipiell den Einfluss
menschlichen Handelns auf die Struktur der
Energieversorgung aufzeigen. Die Ergebnisse der
numerischen Integration von Gleichungen (2,3) sind
in der Abbildung rechts dargestellt. Aus dem
Vergleich mit der darüber liegenden Abbildung
(Berechnung ohne Einfluss des Energiepreises) lassen
sich die folgenden Schlüsse ziehen, welche im
übrigen nicht wirklich überraschen:
|
 Das Versorgungsmodell mit quadratischer Explorationsfunktion unter Berücksichtigung des Energiepreises. |
1) Im Jahr 2000 habe ich mit der Ausarbeitung der Vorlesung "Die Zukunft unserer Energieversorgung" begonnen und hatte keine Kenntnis von der "Hubbert linearisation" oder der "logistic curve", welche in der USAmerikanischen Literatur zur Beschreibung des Erdölabbaus verwendet werden. Hierbei handelt sich um nichts anderes als verschiedene Worte für die gleichen Sachverhalte, die in diesem Kapitel diskutiert werden. Ich sehe deswegen auch keinen Anlass, meine hier und in
2) Ein Beispiel für das stimulierte Wachstum habe ich in
3) Der Explorationsterm des epidemischen Wachstums verletzt diese Bedingung. Daher gilt die Differentialgleichung (1) nur für 0
 t,
wie auch in der obersten Abbildung hier oder in
t,
wie auch in der obersten Abbildung hier oder in 